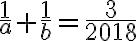Un Défi d'Excellence Mathématique
Chaque
année, le premier samedi de décembre, des étudiants de tout le
continent nord-américain se réunissent pour participer à l'une des
compétitions mathématiques les plus prestigieuses : la Putnam
Mathematics Competition. Créée en 1938 par l'Association mathématique
d'Amérique (MAA), cette compétition est devenue un véritable rite de
passage pour les passionnés de mathématiques.
Qu'est-ce que la Putnam Mathematics Competition ?
La Putnam Competition est une épreuve de six heures divisée en deux sessions de trois heures chacune. Les participants doivent résoudre douze problèmes de mathématiques extrêmement complexes, allant de l'algèbre à la théorie des nombres, en passant par la géométrie et l'analyse. Ce qui rend cette compétition unique, c'est non seulement le niveau de difficulté des problèmes, mais aussi l'accent mis sur la créativité et l'ingéniosité dans les solutions
Pourquoi cette compétition a-t-elle un tel succès ? Pourquoi les étudiants y participent-ils ?
- Développement des Compétences : La Putnam permet aux étudiants de développer des compétences analytiques et de résolution de problèmes à un niveau très avancé, renforçant ainsi leur capacité à aborder des défis mathématiques complexes.
- Reconnaissance et Opportunités : Les meilleurs participants reçoivent des récompenses monétaires, des bourses d'études et des opportunités de stages dans des institutions prestigieuses. La réussite à cette compétition est un atout considérable pour leur avenir académique et professionnel.
- Réseautage et Camaraderie : La compétition est une occasion unique de rencontrer des étudiants et des professeurs partageant les mêmes intérêts. Elle favorise la création de réseaux professionnels et académiques, tout en cultivant un esprit de camaraderie parmi les passionnés de mathématiques.
D'autres Compétitions Mathématiques à Travers le Monde
La
Putnam Mathematics Competition n'est pas la seule compétition de haut
niveau pour les passionnés de mathématiques. En France, les Olympiades de Mathématiques offrent aux lycéens l'opportunité de se mesurer à des problèmes mathématiques stimulants, tandis que le Concours Général de Mathématiques est une épreuve prestigieuse pour les meilleurs élèves des classes de première et de terminale.
À l'échelle mondiale, les International Mathematical Olympiad (IMO)
sont la référence ultime pour les jeunes mathématiciens du secondaire.
Cette compétition annuelle réunit des participants de plus de 100 pays,
leur permettant de tester leurs compétences dans un contexte hautement
compétitif. Il y a aussi l'Asian Pacific Mathematics Olympiad (APMO) et l'European Girls' Mathematical Olympiad (EGMO), qui offrent des plateformes spécialisées pour divers groupes d'élèves.
Ces compétitions, tout comme la Putnam, ne
sont pas seulement des épreuves de connaissances, mais un véritable
défi intellectuel qui pousse les participants à innover et à penser
différemment.
Chez
Lavni, c'est le défi intellectuel que nous voulons retenir au delà du
format "compétition" auquel nous préférons la coopération et l'entraide.
Nous encourageons néanmoins tous les étudiants passionnés de
mathématiques à relever des défis et à explorer les limites de leur
potentiel, dans ce cadre ou un autre.
Êtes-vous prêt(e) pour la Putnam ?
- Alice et Bob jouent à un jeu où ils choisissent tour à tour des entiers de 1 à n. Avant que des entiers ne soient choisis, Bob sélectionne un objectif de "pair" ou "impair". Au premier tour, Alice choisit l'un des n entiers. Au deuxième tour, Bob choisit l'un des entiers restants. Ils continuent à choisir alternativement l'un des entiers qui n'a pas encore été choisi, jusqu'au nième tour, qui est forcé et met fin au jeu. Bob gagne si la parité de {k : le nombre k a été choisi au kème tour} correspond à son objectif. Pour quelles valeurs de n Bob a-t-il une stratégie gagnante ?